Wat zijn de verschillen, en waarom doet het ertoe?
Deze termen worden vaak gebruikt in verschillende context. Soms heeft men wel enig idee wat het ongeveer betekent, maar echt snappen waar nu precies de verschillen zitten doen maar weinig mensen. Doorgaans is het ook van weinig belang, maar een enkele keer maakt dit het verschil.
Geometrie
Met geometrie bedoelen we heel eenvoudige wiskundige figuren: punten, lijnen en vlakken. In wiskundige zin zouden we kunnen stellen dat Geometrie enkel betrekking heeft op een cartesiaans (en dus ook orthogonaal) assenstelsel. Dat betekent heel simpel dat we over 2D of 3D praten, waar de assen (horizontaal, verticaal en hoogte of x, y en z) loodrecht op elkaar staan (precies onder 90 graden), en dat ze dezelfde eenheid hebben, zoals “meter”.
Deze 3 basis-typen (punt, lijn en vlak) kunnen ook samengesteld worden tot meer complexe figuren zoals multipolygonen. In wezen is dat slechts een ingewikkelde term om aan te geven dat meerdere vlakken samen een wiskundige figuur vormen. Kort door de bocht als voorbeeld: een vlak met een gat erin. Dat zijn formeel 2 ringen van willekeurige vorm, waarin de ene ring geheel binnen de andere ligt. Die samenstelling van ringen kunnen we vervolgens interpreteren als een multipolygoon, waarbij de binnenste ring een gat aangeeft in het vlak gevormd door de buitenste ring.
Er zijn heel veel varianten qua bewoording van deze 3 primaire structuren. Uiteraard de Engelse bewoording van node, line en polygon, maar ook varianten op de laatste zoals area of surface. Soms worden die twee laatste termen weer gebruikt om specifiek multi-polygonen te benoemen.
Als je dit fundamenteel beschouwt, of eerder vanuit ICT-perspectief, zou je kunnen stellen dat er slechts 2 structuren bestaan: punten (nodes) en ketens van punten (ways). Verder heb je dan enkel nog relaties van meerdere geometrieën nodig, dus samenstellingen van nodes en ways als relation. Dit is precies de insteek die men aanhoudt in het OpenStreetMap datamodel. Hierbij geldt dat een keten van punten met een gelijk begin- en eindpunten als gesloten (of closed) wordt beschouwd, en daarmee dus ook gelijk een vlak of polygoon beschrijft.
Vanwege de beperkingen in toepassingsruimte tot een cartesiaans assenstelsel, is het relatief eenvoudig om meetkunde toe te passen op de figuren, bijvoorbeeld om de oppervlakte of lengte van een geometrie te berekenen.
Geografie
Hoewel geografie uiteraard een algemene term is voor Aardkunde, wordt daar in deze context iets heel specifiek mee bedoeld. Een geografie is de wiskundige ruimte die niet voldoet aan de vereisten van het cartesiaans assenstelsel. Een eenvoudigere verwoording is: “het gaat niet om meters, maar om graden”. De oppervlakte van een geometrie berekenen kan heel eenvoudig, ongeacht de eenheden, vanwege de cartesiaanse eigenschappen. De oppervlakte van een geografie berekenen is veel complexer; daar komt geodesie bij kijken.
Deze betekenis van het relatief courante woord geografie is eerder specifiek, en het onderscheid wordt niet altijd strak aangehouden. Zo is het bijvoorbeeld mogelijk om met gegevens in graden te werken, en te “doen alsof” dit een cartesiaans assenstelsel betreft. Daar zijn dan weer datatechnische motieven voor. In dit artikel willen we dus de term geografie neerzetten voor ruimtelijke figuren die niet cartesiaans zijn, en dus formeel geen geometrie. Dat dit conceptuele onderscheid vaak maar beperkt relevant is, nemen we even voor lief.
Geodesie
Geodesie is de wetenschap die zich bezig houdt met de vorm van de aarde. Dat is niet “zomaar” een bol, maar een oblate sferoïde. Wederom een moeilijke term om het simpele feit te benoemen dat de aarde wat platgeslagen is op de polen. De diameter van de aarde op de evenaar (equatoriaal; 12.756 km) is groter dan de “verticale” diameter over de polen (polair; 12.714 km). Deze afplatting valt uit te drukken als 1 op 300.
Daarnaast moet in het model van de aarde (dat we een geoïde noemen) ook rekening gehouden worden met de zwaartekracht. Waarom dat zo is, kan best geïllustreerd worden met volgend gedachten-experiment;
Stel je voor dat de aarde bijgevuld wordt met een extreme hoeveelheid water, waardoor alle bergen ruim onder water komen te staan. Wat zou dan de vorm van die “bal water” zijn? Laten we daarbij ook even aannemen dat er geen effect is van getijden of planetaire beweging door het zonnestelsel. Men is geneigd dan te denken dat we een perfecte bolvorm (cirkel) zouden hebben. Nog los van het bovenstaande punt over de oblate sferoïde, is het zo dat zwaartekracht daar wel nog een aanzienlijke invloed op heeft. Daar waar er in de ondergrond een grote hoeveelheid ijzer zit, is de zwaartekracht namelijk groter. Het effect daarvan is vervolgens dat we een “put” of indeuking van het wateroppervlak krijgen. De Engelse term hiervoor is “dimple”. Het water-oppervlak is ook dan niet perfect “glad”.
Dit effect is niet iets wat enkel optreedt in dat soort theoretische gedachten-experimenten. Het is daadwerkelijk al gemeten in grote oppervlakten van meren en dergelijke.
Maar waarom is dat nu van belang? Is dat niet gewoon verwaarloosbaar tegenover het rimpelend effect van de getijden en het weer?
Ja en nee. Het gaat inderdaad over bijzonder kleine effecten, die nu voor het eerst goed meetbaar worden met laser-altimetrie (LIDAR). Dat is weer een dure formulering van: een vliegtuig dat met een laser de hoogte heel precies meet. Dus ja, het gaat over best wel kleine effecten. Toch is dat erg relevant voor de computermodellen die water-stromingen berekenen. Denk bijvoorbeeld aan de modellen die voorspellen hoe we de stuwen moeten afstellen om water te lozen (of juist op te houden) afhankelijk van het weer, en verwachtte instroom van water hogerop op een rivier. Voor dergelijke modellen zijn deze effecten niet verwaarloosbaar, al helemaal niet als je voor een groot meer sensoren hebt die de water-hoogte rapporteren. Daar kan dan een zeer klein verschil optreden die lijkt te wijzen op een aanstaande tsunami, terwijl het in werkelijkheid de stabiele situatie is.
Dus samengevat; geodesie gaat over de vorm van de aarde. Dat is véél complexer dan gewoon 1 keer nauwkeurig de diameter van de aarde op te meten. Het is met deze geodetische informatie dat gegevens van een geografie kunnen worden omgezet naar een geometrie.
Oké, allemaal leuk en aardig voor theoretische modellen, maar Bob de Bouwer heeft hier toch nooit mee te maken?
Dat ligt (gek genoeg) toch vrij genuanceerd. Bij het bouwen van een individuele woning, hoef je uiteraard geen rekening te houden met afwijkingen in het lokale zwaartekrachtveld. Maar dat geldt niet overal. Bij de aanleg bijvoorbeeld van enorme industriële kades in de haven van Delfzijl, heeft dit fenomeen wel degelijk voor problemen gezorgd voor onze Bob! Er trad namelijk een aanzienlijk verschil op (nou ja, eigenlijk heel klein, maar toch relevant voor dat soort infrastructuur) tussen de met een theodoliet bepaalde hoogte van de kade over enorme afstand, en de feitelijke afstand ten opzichte van het water. Nu heeft dat meer te maken met het onderscheid tussen 2D-geometrie, en kromming van de aarde in een geografie, maar het principe staat wel degelijk. Er zijn legio voorbeelden waar deze soms zeer subtiele geodetische aspecten zeer relevant bleken voor onze Bob.
Topologie
Met topologie wordt de onderlinge verhouding in ligging tussen 2 ruimtelijke figuren bedoeld. Bijvoorbeeld: A ligt in B. Of A doorsnijdt B. Of A raakt B. Deze termen van “in”, “doorsnijdt” of “raakt” zijn topologische predicaten, die een topologische interactie benoemen. Er zijn steeds 3 aspecten van een geometrie die zich verhouden tot de 3 aspecten van de andere geometrie, resulterend in 9 interacties. Deze 3 aspecten zijn Interior (de oppervlakte), Boundary (de begrenzing) en Exterior (alles buiten die geometrie). Dergelijke topologische interacties zijn bijvoorbeeld uitgewerkt in het DE-9IM (het Dimensionaly Extended 9-Intersection-Model) van Clementi, gebaseerd op de fundamenten zoals Egenhofer die heeft vastgelegd.

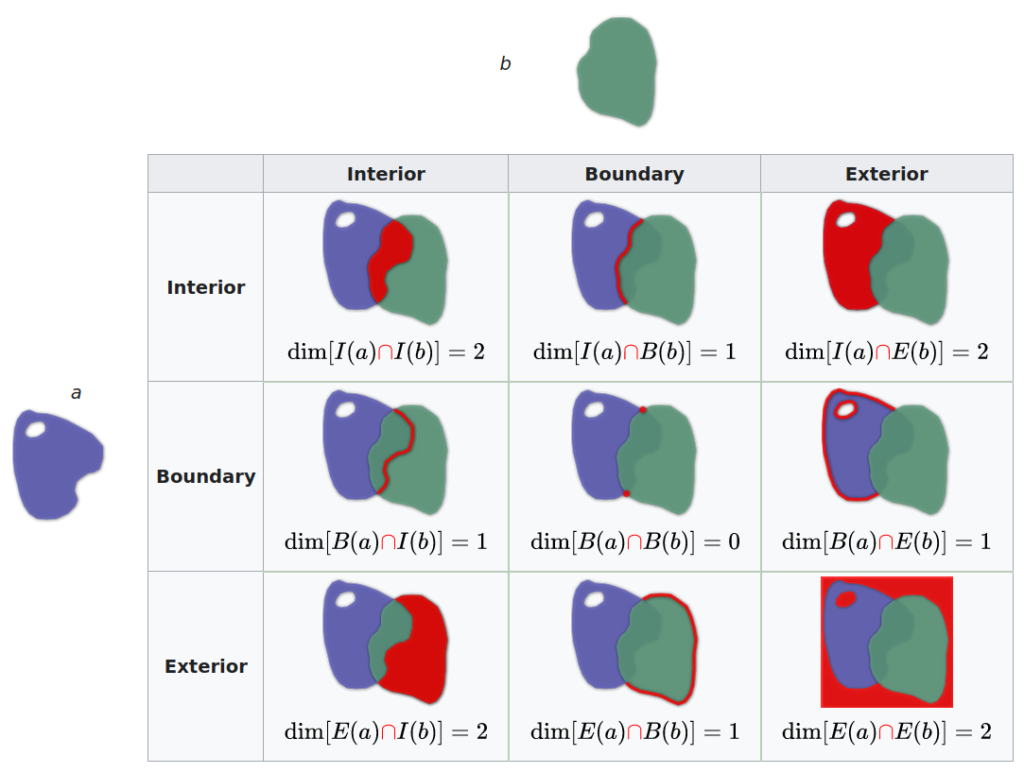
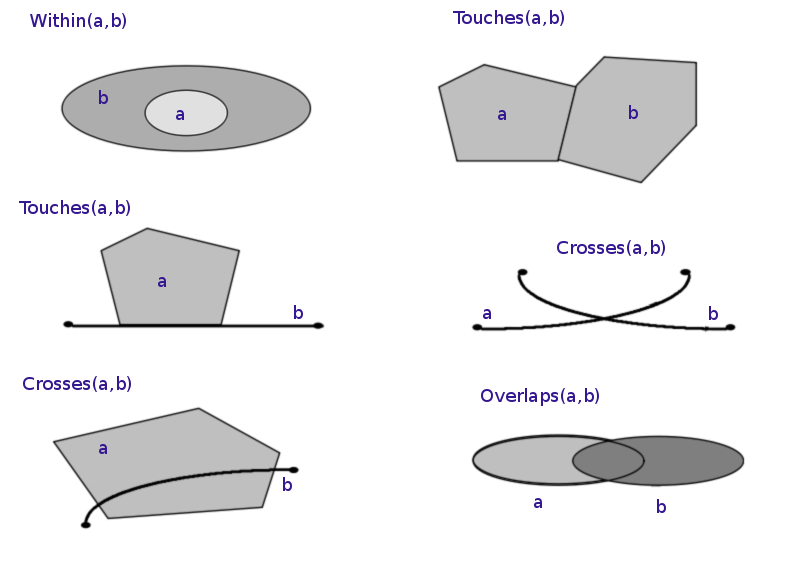
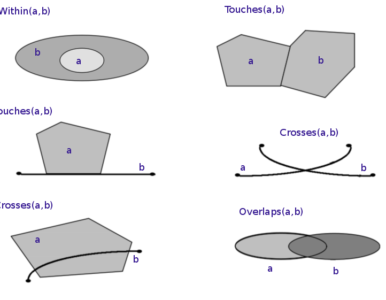
Uit de 9 mogelijke relaties zoals beschreven in het DE-9IM, volgen een aantal ruimtelijke predicaten, die de abstracte elementaire topologische verhoudingen beschrijven;
- Equals: gelijk aan; de twee entiteiten zijn topologisch identiek.
- Disjoint: de twee geometrieën zijn niet met elkaar verbonden.
- Touches (meets): de twee geometrieën raken elkaar in minstens 1 punt (dat kan dus ook een lijn zijn), maar hun oppervlaktes overlappen niet.
- Contains: bevat; de ene geometrie b bevat de andere, als deze geheel binnen deze geometrie ligt, en met minstens 1 punt de rand van die geometrie raakt.
- Covers: bedekt; de meer algemene relatie dan contains, omdat de 2 geometrieën elkaar niet hoeven te raken.
- Intersects: de 2 geometrieën hebben minstens 1 punt gemeenschappelijk. Dit impliceert ook Touches.
- Crosses: doorkruist; de geometriën hebben een deel van de oppervlakte gemeenschappelijk, maar niet het volledige oppervlak. Dat betekent dus dat beide geometrieën deels buiten elkaar liggen, en deels overlappen.
Daar waar het DE-9IM deze topologische relaties beschrijft vanuit de interactie tussen 2 geometrieën, beschrijft het RCC8 (Region Connection Calculus) deze interactie vanuit de gebieden zelf. Volgende 8 eigenschappen worden onderscheiden.
| code | naam | Nederlands | omschrijving |
|---|---|---|---|
| DC | disconnected | losgekoppeld | de twee gebieden raken elkaar niet |
| EC | externally connected | rakend aan de buitenzijde | de twee gebieden raken elkaar aan de buitenzijde (op een punt of lijn) |
| EQ | equal | gelijk | de twee gebieden zijn gelijk aan elkaar |
| PO | partially overlapping | gedeeltelijk overlappend | de twee gebieden overlappen elkaar gedeeltelijk (vlak als interactie) |
| TPP | tangential proper part | ingesloten rakend | het tweede gebied ligt binnen het eerste gebied, en raakt deze op de buitenzijde |
| TPPi | tangential proper part inverse | ingesloten rakend (omgekeerd) | zelfde als TPP, maar in omgekeerde volgorde (eerste gebied ligt binnen tweede gebied) |
| NTPP | non-tangential proper part | ingesloten vrij liggend | het eerste gebied ligt binnen het tweede gebied en raakt deze niet |
| NTPPi | non-tangential proper part inverse | ingesloten vrij liggend (omgekeerd) | zelfde als NTTP, maar in omgekeerde volgorde |

Maak je het nu niet veel te ingewikkeld en wiskundig, en gaat topologie in deze context niet gewoon over “gaps and overshoots”?
Nee. Topologie is de wetenschap om de relaties tussen geometrieën te beschrijven. Dit heeft heel veel afgeleide informatie-aspecten, zoals logic inference in linked data. Het afleiden van die wiskundige predicaten is van groot belang om zeer alledaagse concepten in spreektaal te kunnen vertalen naar effectieve technische concepten. We staan er niet bij stil, maar in heel veel zaken waar we iets zeggen over een Plaats, gebruiken we daar topologische predicaten bij. Bijvoorbeeld, om aan te geven dat we “Valkenburg in Zuid-Holland” bedoelen, en niet Valkenburg in Limburg. Dat logische predicaat “in” is niet triviaal, en het is van groot belang om dergelijke zaken heel scherp te kunnen vatten in allerlei systemen. Dat geldt zowel voor structurele data-opslag als voor de UI (User Interface).
Het klopt dat dit een operationele weerslag heeft in veel GIS-software in de zin dat “werken aan topologie” vaak hetzelfde betekent als het oplossen van “gaps and overshoots” maar dat is dus slechts 1 operationele bijzaak, en verre van de essentie van waarom we zaken doen. Een ander fundamenteel aspect is namelijk hoe je de topologische data-opslag regelt van zaken, zodat het afleiden van logische relaties tussen entiteiten altijd verzekerd kan worden.
Daar waar in regulier Desktop-GIS-software zoals ArcGIS en QGIS die topologische klussen grotendeels bestaan uit software-matige beperkingen opleggen en handhaven (dus: het oplossen van die “gaps and overshoots”), is dat niet de de kern in datatechnische zin. OpenStreetMap raakt deze kern wél met hun datamodel, dat eerder ICT-logisch geïnspireerd is dan vanuit operationeel GIS. Het fundamentele verschil zit bijvoorbeeld in aangrenzende vlakken die een stuk grens gemeenschappelijk hebben. In regulier GIS kun je dus allerlei zaken afdwingen met checks dat die lijnen zo goed mogelijk op elkaar liggen, maar dat blijft een softwarematig afgedwongen logica. Het is niet een basale eigenschap. Dat betekent ook dat in complexe randgevallen, het soms kan voorkomen dat de topologische integriteit verloren gaat, als je wisselt naar een andere projectie.
De insteek vanuit OpenStreetMap bouwt alles dus door vanuit een node als basis-entiteit met een coördinaat. Lijnen zijn dan gewoon ketens van verwijzingen naar diezelfde nodes. En vlakken zijn dan gesloten ketens van nodes, met dus hetzelfde begin- en eindpunt van de keten. Ook de complexe samengestelde geometrieën zijn in wezen niets anders dan verwijzingen naar die nodes. Dat is een fundamenteel punt, omdat topologische integriteit dan ook fundamenteel een onderdeel is van de data-structuur. Dat verandert overigens helemaal niets aan de noodzaak om ook in zo’n model de nodige checks te laten bestaan op topologische fouten.
Al brengt ons dat wel op een slippery slope, van “wanneer is een geometrie fout?”. Misschien is een overlap ergens juist wel bedoeld. Dat kan best, bijvoorbeeld conceptueel met huizen die “op” percelen staan, en ze dus overlappen.
Deze hele discussie is geen punt het de hoogste deugd met het nastreven van het hoogste niveau nastreven van oplossen van kleine gaps en overshoots, hoewel dat wel altijd een lovenswaardig doel is. Fundamenteel komt er in uitgebreide systemen vaak op neer dat je zaken eenduidig kunt registreren, en niet onderhevig bent aan willekeur. Daarmee bedoel we; willekeur inzake het al dan niet in overeenstemming zijn met een aantal logische checks afhankelijk van de arbitrair gekozen projectie.