Soms worden allerlei termen door elkaar gebruikt; vlak, polygoon, perceel, etc. Maar wat is nu de juiste naam? En wat is het verschil, en waarom zijn er zo veel verschillende namen om hetzelfde aan te duiden?
Semantiek: de inhoudelijke betekenis
Als je mensen vraagt wat ze in een Geografisch Informatie Systeem (GIS) tekenen, dan krijg je vaak de semantische entiteit te horen. Men tekent huizen, wegen, rivieren, bergen en percelen. Het ligt voor de hand dat ongeacht het technische systeem, veel gebruikers primair een inhoudelijk doel hebben, van het tekenen van die entiteiten. Dat is natuurlijk helemaal prima, maar ook technisch niet precies. Je tekent namelijk geen “percelen”, maar je tekent een vlak, dat je vervolgens de eigenschappen toekent die stellen dat het een perceel betreft. Dat is de bottom-up definitie van entiteiten zoals ze worden aangehouden voor Linked Data.
Klassiek desktop GIS (zoals QGIS of ArcGIS) werkt anders. Daar definieer je eerst een laag als semantisch homogene entiteiten, en teken je daarna de entiteiten, die daarmee allemaal van dat type zijn. Bijvoorbeeld; je maakt een laag met lijn-elementen, en daarvan stel je dat het rivieren zijn. Je geeft ze vervolgens in de attribuut-tabel de “kolommen” die logisch zijn voor die entiteit, zoals bijvoorbeeld een kolom die de naam van de rivier aangeeft. Dat heet een top-down benadering, omdat 1 keer aan het begin wordt gesteld wat de entiteiten precies zijn, en waar ze aan moeten voldoen.
Werken met lagen als entiteit-types is handig voor de grafische weergave. Je kunt dan bijvoorbeeld instellen dat alle rivieren worden weergegeven als blauwe lijn. Maar het is tegelijkertijd ook onhandig, want een entiteit kan niet tot 2 lagen behoren. Je kunt natuurlijk een kopie van een entiteit in beide lagen hebben, maar conceptueel ligt er dan niet noodzakelijk een verband. Dat is de belangrijkste reden waarom dit paradigma niet wordt gevolgd door systemen als OpenStreetMap. Daarbij kan een entiteit meerdere zaken zijn, afhankelijk van de individuele tags die de entiteit bezit.
Bijvoorbeeld; een vlakje is een gebouw, als deze een tag building bezit. Datzelfde vlakje kan ook iets anders zijn, zoals een perceel. Of een rivier. Niets houdt je tegen (buiten conventies en afgedwongen regels) om een vlakje zowel een gebouw als een rivier te maken. Als je dat onlogisch vindt, moet je operationele logica schrijven die dat verbiedt, of minstens een waarschuwing geeft.
Technisch: it’s all about the nodes, stupid!
Als we technisch naar getekende objecten kijken, is er grosso modo maar 1 basale entiteit: een node of punt. Een puntlocatie heeft een coördinaat (in eender welk stelsel, op aarde, of desnoods op de maan).
Lijnen (OSM: ways) zijn ketens (arrays) van punten. De individuele nodes hebben een volgnummer in een lijn, en de lijn heeft een richting waarin de punten elkaar opvolgen. De tussenliggende punten van een lijn, tussen het begin- en eindpunt, worden ook wel de knooppunten (1 vertex of meerdere vertices) genoemd. Dat is synoniem met node / punt, met het subtiele verschil in nuance dat vertex vooral wordt gebruikt om conceptueel een tussenliggend knikpunt te benoemen dat geen verdere eigenschappen heeft (zoals begin- of eindpunt van een lijn).
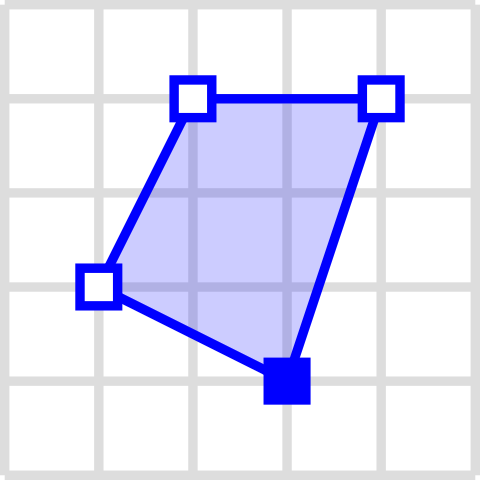
Vlakken zijn technisch gewoon weer ketens van punten, met hetzelfde begin en eindpunt. Ze beschrijven daarmee een oppervlakte.
Uitzonderingen
De beschrijving hierboven geldt voor basale data-gedreven geometrie-structuren. Een veelvoorkomende structuur (vooral uit de CAD-wereld) is namelijk deze van een “curve”, waar elk cirkel-segment in de regel wordt beschreven door precies 3 punten: beginpunt, eindpunt, en dikte van de buik van de curve. Dat soort structuren (en allerlei creatieve alternatieve structuren) worden doorgaans niet goed in GIS-software gerepresenteerd. Het probleem zit namelijk in het gegeven dat een curve (of andere niet-punt gebaseerde geometrieën) enkel betekenis hebben in een Euclidische Ruimte.
Vertaald naar de betekenis binnen geografie, betekent dat bijvoorbeeld dat de curve drastisch kan wijzigen als je de kaart alleen nog maar weergeeft in een andere projectie. Daarvoor is het voor data-gedragen systemen erg onwenselijk om structuren te gebruiken die een afhankelijkheid hebben ten aanzien van dergelijke projectie-specifieke zaken. Daarom laten we deze verder buiten beschouwing hier.
Complexere structuren afgeleid van punten
Naast de reguliere geometrie-vormen, zijn er ook complexe, samengestelde vormen van een geometrie. Deze worden vanwege deze samengestelde vorm ook wel multi-geometrieën genoemd. De meest gekende soort zijn multi-polygonen, maar er zijn ook multi-linestrings en multi-nodes.
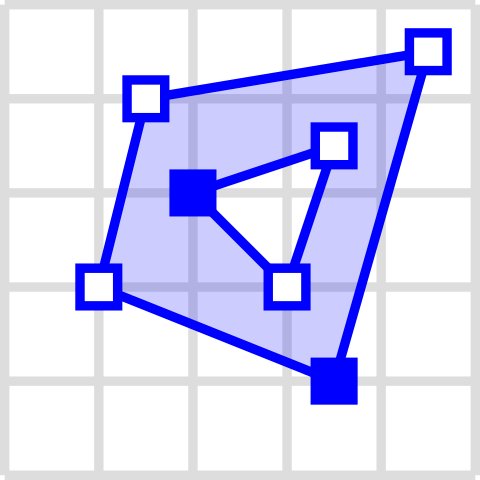
Meest basale vorm van een multi-polygoon, bestaande uit twee ringen (de binnenring en de buitenring), elk weer bestaande uit een reeks knooppunten met hetzelfde begin- en eindpunt (blauw gevuld weergegeven). Bron: Wikimedia.
De meest eenvoudige vorm hiervan bestaat uit twee polygonen die met enige ruimte ertussen naast elkaar liggen, en elkaar niet raken. In zekere zin zijn dat twee reguliere, losse, polygonen, maar de multi-polygoon bestaat zodat je kunt uitdrukken dat die geometrie in zijn geheel 1 feature uitdrukt. Een ander veelvoorkomend voorbeeld, zijn reguliere vlakjes “met een gat”. Dit kan bijvoorbeeld een vijver zijn in een tuin, een drinkwaterpoel in een weiland, etc. Beide soorten multi-polygonen zijn aan elkaar gerelateerd. Dat wordt het meest duidelijk als je denkt aan het voorbeeld van enclaves en exclaves, waar de ene figuur een losliggend deel heeft, maar het andere deel weer een gat bevat waar dat stukje van die eerste in ligt.
In de context van het beschrijving van die geometrische figuur spreken we ook van ringen van een multi-polygoon. Dat kan een binnenring zijn (zoals in het geval van een “gat” in een structuur) en dat kan een buitenring zijn. Het kunnen ook meerdere ringen zijn van eender welk type multi-polygoon.
In reguliere GIS-omgevingen zijn dit complexe structuren, met zeer uiteenlopende “regels” die bepalen hoe een multi-polygoon moet worden opgebouwd. Zo geldt bijvoorbeeld soms dat de richting van vertices in een ring (met de klok mee versus tegen de klok in) precies tegenovergesteld moet zijn tussen de binnenring en buitenring. Soms geldt die regel niet. Dit hangt weer samen met of het is toegestaan dat de ringen van een multi-polygoon elkaar raken.
Soms wordt daarbij ook onderscheid gemaakt met of de buitenring de binnenring mag raken, of dat meerdere binnenringen elkaar mogen raken. Dat klinkt aanvankelijk wellicht als een zeer vergezocht voorbeeld, maar in realiteit komt dit vaak voor. Denk bijvoorbeeld aan een perceel, met in het midden niet 1 perceel, maar 2 percelen die tegen elkaar liggen. Je kunt dat omvattende perceel dan representeren met 1 buitenring en 1 binnenring (als lijn die over die andere percelen heen ligt, of als een buitenring met twee binnenringen.
In de OpenStreetMap terminologie gaat men hier op een meer abstracte wijze mee om. Alle complexe samengestelde figuren worden relaties genoemd. Zo’n relatie kan een multi-polygoon zijn, maar ook een willekeurige andere samenstelling van elementen. Bijvoorbeeld, je zou een land kunnen representeren als een buitenring als gesloten lijn, met ook 1 punt op de locatie van de hoofdstad. De “rol” die de leden van een relatie spelen kan dan ook heel simpel “inner” of “outer” zijn (zoals bij een klassieke multi-polygoon), maar kan ook arbitrair gekozen worden. Een ander klassiek voorbeeld van relaties zijn de Openbaar Vervoer-routes, als een verzameling van fysieke wegen als een multi-linestring.
In een klassieke GIS-omgeving is een multi-geometrie een losse entiteit, die geen adresseerbare onderdelen bevat. Als je dus een multi-polygoon-laag hebt, is alles een multi-polygoon als type, ook als dit maar 1 buitenring bevat. Vanwege de samengestelde structuur van OpenStreetMap-gegevens, ligt dat heel anders.
Neem als voorbeeld een rechthoekig perceel, met in het midden (met enige afstand tot de zijden) een ingesloten perceel. Conceptueel teken je in zo’n geval twee gesloten lijnen, die dus allebei een oppervlak uitdrukken, en als gesloten lijn ook synoniem zijn met een vlak. Die binnenring is dan in zijn basale structuur ook een inhoudelijk perceel met een grondgebruik. Voor de buitenring geldt dat niet, anders zou het buitenste perceel het binnenste overlappen. Het is daarom de relatie als uitdrukking van de multi-polygoon van het omvattende perceel, dat dat eigenlijke buitenste perceel uitdrukt. Dat betekent dus dat alle eigenschappen (tags) van het perceel NIET op die buitenring mogen worden geplaatst, maar enkel gelden voor de relatie.
Je hebt in dat voorbeeld dus 2 geometrieën getekend: een buitenring zonder tags, en een binnenring die de tags van dat ingesloten perceel bevat. Daarnaast is er dus de relatie die uitdrukking geeft aan dat omvattende perceel, en dus ook de tags van dat perceel krijgt.
Soms is er ook sprake van een complex samenspel. Stel bijvoorbeeld dat je 1 rechthoekig perceel hebt (met als adres Sectie A, perceelnummer 100) met daarin een getekende drinkwaterpoel, die geen los perceelnummer heeft gekregen, en dus gewoon onderdeel is van datzelfde perceel. In dat geval krijg je dus weer dezelfde multi-polygoon als relatie in OpenStreetMap. De buitenring is in dat geval het volledige perceel met het kadastrale adres. De relatie (dus het omvattende vlak) het gedeelte met landuse-meadow als tag, en de drinkwaterpoel als inner-ring is dan heel simpel natural=water. Het administratieve perceel blijft in die gevallen de buitenring, die dus verder geen grondgebruik als codering draagt.
Deze structuur heet in de formele logica distributief. Dat kennen we uit de wiskunde in het simpele voorbeeldje van 2 * (3 + 4) (of dus: 2 keer drie plus vier). Door de haakjes is die vermenigvuldiging distributief. Dat betekent dat die som (met als uitkomst 14), logisch equivalent is aan (2 * 3) + (2 * 4). Want dat is 6 + 8, of dus ook 14. Die abstracte wiskundige eigenschap, geldt ook voor de relatie van de multi-polygoon. Het gegeven voorbeeld van buitenring als perceel, met dan de relatie als weiland, en de binnenring als water, is logisch equivalent aan de alternatieve uitdrukking van het laatste voorbeeld in 2 percelen: de relatie (of dus multi-polygoon) als weiland, met de eigenschappen van het kadastraal adres, en de binnenring óók met de uitdrukking van datzelfde kadastrale adres. De buitenring blijft in dat geval zonder tags of eigenschappen.
Er is geen logisch verschil tussen beide uitdrukking, ze zijn formeel-logisch equivalent. Dat betekent ook dat er geen goede of foute manier is om het uit te voeren. Maar hoe dan ook zul je in dat voorbeeld een relatie nodig hebben, om uitdrukking te geven aan die buitenring als grondgebruik, of als onderdeel van het perceel met expliciete tags.
Als HisGIS hebben we ervoor gekozen om deze formele logica ook als basisregel aan te houden. Daarmee breken we zeer expliciet met het uitgangspunt en nobele streven dat 1 perceel ALTIJD uit 1 geometrie moet bestaan bij het intekenen. Dat lijkt aanvankelijk misschien als een meer zuivere insteek, maar het bestaan van sub-delen (perceel-delen) van een perceel, is onvermijdelijk in de praktijk.
Denk bijvoorbeeld aan het voorbeeld dat 1 groot perceel, doorloopt over meerdere minuutplans. Je moet dan middels de tag kad:blad het nummer van het minuutplan in die sectie coderen, maar daarvoor moet je het perceel noodzakelijkerwijs in twee knippen om die afzonderlijke kad:blad tag toe te kunnen voegen. Je zou ervoor kunnen kiezen om twee gesloten lijnen als vlakjes in te tekenen met hetzelfde perceelnummer, en dat is prima. Je zou er ook voor kunnen kiezen om die vlakjes enkel te voorzien van de respectievelijke kad:blad tag, en dan vervolgens een relatie aan te maken met beide vlakjes als aan-elkaar-grenzende buitenringen als leden. Beide structuren zijn logisch equivalent. Er is geen juiste of foute oplossing.
Het gekozen voorbeeld komt in de praktijk niet extreem vaak voor. Veel couranter is de structuur waarbij een weiland, ook administratief de halve aangrenzende sloot “bevat”. Dat brengt de haast filosofische discussie met zich mee of weiland als grondgebruik van het perceel ook de halve sloot omvat. Die filosofische discussie is niet heel relevant voor de administratieve werkelijkheid. Het perceel is omschreven als bevattende ook de halve sloot. Punt. Op de kaart kan die sloot duidelijk zijn weergegeven als ingekleurd blauw vlakje (langgerekt). Dus in zo’n geval is de richtlijn om beide als een los perceel te tekenen met een eigen kadastraal adres en eigen grondgebruik. Uiteraard wel met hetzelfde kadastrale perceelnummer. Je hoeft in zo’n geval niet te klooien met complexe relatie-structuren om een multi-polygoon uit te drukken.
Als je dat wel zou doen voor een perceel (dat dan dus steeds uit 2 sub-vlakjes bestaat; eentje voor het weiland, en eentje voor de halve sloot), waarom zou je voor al die stukjes halve sloot ze niet moeten samenvoegen in 1 relatie om dat grondgebruik centraal te coderen als water? En waarom zou je dat niet moeten doen voor elke gemeente, waarbij die relatie per gemeente ENKEL een tag bevat om de kadastrale gemeente aan te geven, maar die relatie weer lid is van een andere relatie die al die halve slootjes over verschillende gemeenten heen aan elkaar verbindt met op 1 centrale plek dat grondgebruik van natural=water? Ook al die absurde constructies zijn logisch equivalent, maar uiterst onhandig om mee te werken. Daarom dus het uitgangspunt dat we zo weinig mogelijk relaties gebruiken, waar het ook eenvoudig met dubbele tags om meerdere onderdelen te benoemen kan.